Electromagnétisme à régimes variables
Le régime variable correspond aux formes finales des
Equations de Maxwell. Ce sont les équations du
Magnétostatisme et de l'
Electrostatisme avec l'ajout de la dépendence temporelle.
Induction électromagnétique
Le phénomène d'induction électromatique apparaît dans un circuit en mouvement situé dans un champ magnétique constant ou alors dans un circuit fixe situé dans un champ magnétique variable.
Loi de Faraday
Loi de Lenz
Relation de Maxwell-Faraday
Equations de Maxwell
On s'intéresse au cas des régimes variables dans le temps.
$$\vec{rot}(\vec E)=-\frac{\partial \vec B}{\partial t}$$
$$\implies \vec E={{-\frac{\partial \vec A}{\partial t}-\vec{grad}(V)}}$$
Avec:- \(\vec A\): potentiel magnétique
- \(V\): potentiel global
:
Démonstration de la relation de Maxwell-Faraday
1
On sait que $${\subset\!\supset} \llap{\iint}_S\vec B.d\vec S=0$$
Cela implique, par
Théorème d'Ostrogradsky - de la divergence, que:
$$div(\vec B)=0$$
Alors:
$$\vec B=\vec {rot}(\vec A)$$
Avec \(\vec A\), un potentiel vecteur
2
$$\vec {rot}(\vec E)=\frac{\partial B}{\partial t}=\frac{\partial (\vec{rot}(\vec A))}{\partial t}$$
2i
$$\vec{rot}(\vec{E}+\frac{\partial \vec A}{\partial t} )=0$$
Alors, il existe un potentiel \(V_G\) scalaire:
Donc:
$$\vec E=-\vec{grad}(V_G)-\frac{\partial\vec A}{\partial t}$$
Applications
- Auto-induction d'une bobine
- Induction mutuelle
- Générateurs électromagnétiques
- Courants de Foucault
Paradoxe de Maxwell
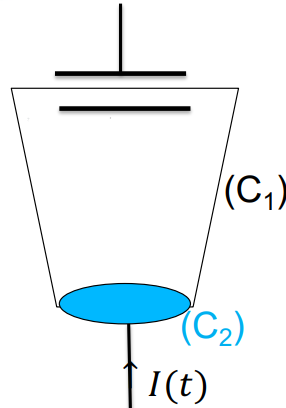
D'aprés le
Théorème d'Ampère, le champ \(\vec B\) peut être:
- \(\vec B = \mu_0I(t)\) pour (\(C_2\))
- \(\vec B = \vec 0\) pour (\(C_1\))
Or, d'après le
Principe de conservation de la charge à densité constante:
$$div(\vec j)=-\frac{\partial \rho}{\partial t}=0$$
Théorème d'Ampère
$$\vec{rot}(\vec B)=\vec j$$
Par définition:
$$div(\vec{rot}(\vec B))=div(\vec j)=0$$
Alors, il introduit: $$\vec j_D=\frac{\partial \vec D}{\partial t}=\epsilon_0\frac{\partial\vec E}{\partial t}$$
Avec:
Finalement:
$$\vec j= \vec j_{Courant}+\vec j_D$$
Il corrige alors l'équation l'équation \(\vec rot(\vec B)=\mu_0 \vec j\):
Equations de Maxwell
Energie électromagnétique
Densité volumique d'énergie électromagnétique
Cette densité est la somme des densités dû à l'Electrostatisme et au Magnétostatisme.
$$e_{em}={{\frac 12 (\vec E.\vec D+\vec B.\vec H)}}$$
Avec:
